- 1번 문제

일단 A가 C보다 순위가 낮으므로, A<C라고 표시해준다.
E의 순위는 B와 A 사이라 했고, B보다 순위가 낮은 사람은 없다고 했으므로 B<E<A<C가 성립한다.
D는 A보다 순위가 높다고 했으므로 B<E<A<D<C 또는 B<E<A<C<D 둘 중의 하나가 순위로 나오는데, 3등만 구하면 되므로 A가 답이 된다.
- 2번 문제

전형적인 dp형 문제이다.
대충 1차원 배열이 있다고 가정한 다음 7번 인덱스, 9번 인덱스, 11번 인덱스에 1을 집어넣고, dp[i-7] || dp[i-9] || dp[i-11]이라면 dp[i]를 1로 만들고 i를 1 증가시키는 반복문을 dp[i-7]부터 dp[i]가 모두 1이 되기 전까지 반복하면 된다.
dp[i-7]부터 dp[i]까지가 모두 1이라면 i가 계속 커져도 7, 9, 11로 수 제작이 가능해진다.
따라서 반복문을 모두 돈 뒤, i-7이 답이 된다.(답 : 27)
- 3번 문제

주어진 직육면체 (2, 5, 8), (4, 4, 9), (3, 2, 4) 중 (3, 2, 4) 직육면체는 어떻게 조합해도 밑면이 다른 직육면체에서 조합 가능한 가장 작은 밑면보다 작으므로 언제나 꼭대기에 있어야 하고, 꼭대기에 있을 때는 바닥 면적이 작을수록 더 유리하므로 (2, 3, 4)이나 (3, 2, 4)로 고정시켜 놓는다.
그 후, 남은 두 직육면체 (2, 5, 8), (4, 4, 9) 중 어느 직육면체를 맨 아래에 놓아야 할지 고민한 결과, (2, "5", 8)이기 때문에 (4, 4, 9)가 밑에 있어야 하고, (4, 9, 4)의 형태로 놓으면 된다는 사실을 알았다.
이렇게 놓았을 땐 (4, 9, 4) 직육면체 위에 (2, 5, 8) 형태로 올려지거나, (2, 8, 5)의 형태로 올려질 수 있는데, 가장 높게 쌓으라고 했으므로 (2, 5, 8)의 형태로 올려야 한다.
이 상태에서 모든 직육면체의 높이만을 더하면 4 + 8 + 4가 나와 답은 16이 된다.
-4번 문제

문제를 시각화하면 다음과 같은 모양이 나올 것이다.

6개월 전에는 이 문제를 직접 노가다로 풀었지만, 실력이 많이 향상된 지금은 그런 무식한 방법은 쓰지 않는다.
일단 문제를 풀기 전 원주에 공이 2개, 4개, 6개 있을 때 각각 쌍을 제작 가능한 경우의 수를 구해야 한다.
구한 결과, 2개일 때는 1개의 경우가 있다.
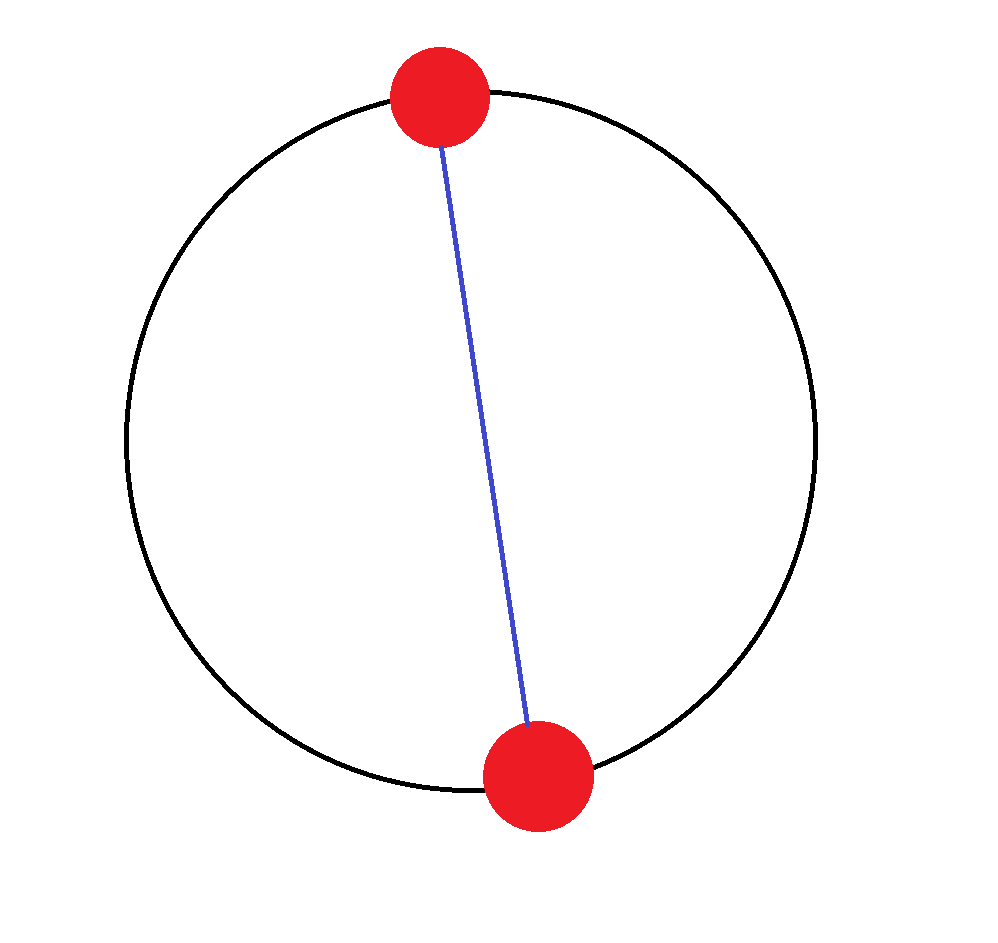
공이 4개일 때는 2가지 경우가 있는데, 여기서부터 점화식을 쓸 것이다.
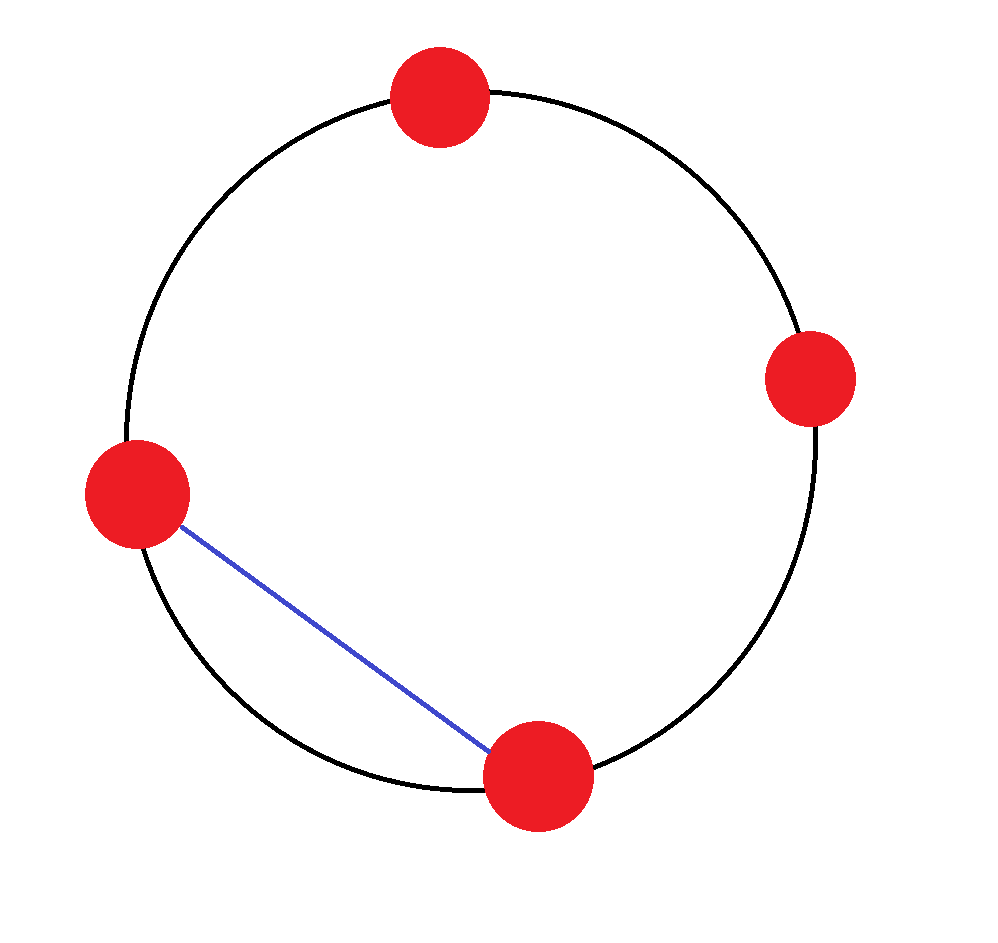
4개 중 2개를 저런 식으로 연결하면 2개가 남는데, 아까 원주에서 공이 2개만 있을 때 쌍을 제작 가능한 경우의 수는 1가지라 했고,

이런 식으로도 이을 수 있으며 이 때도 공이 2개가 남았기 때문에 1가지가 나와 원주에 공이 4개 있을 때는 제작 가능한 쌍의 경우의 수는 2가지가 된다.
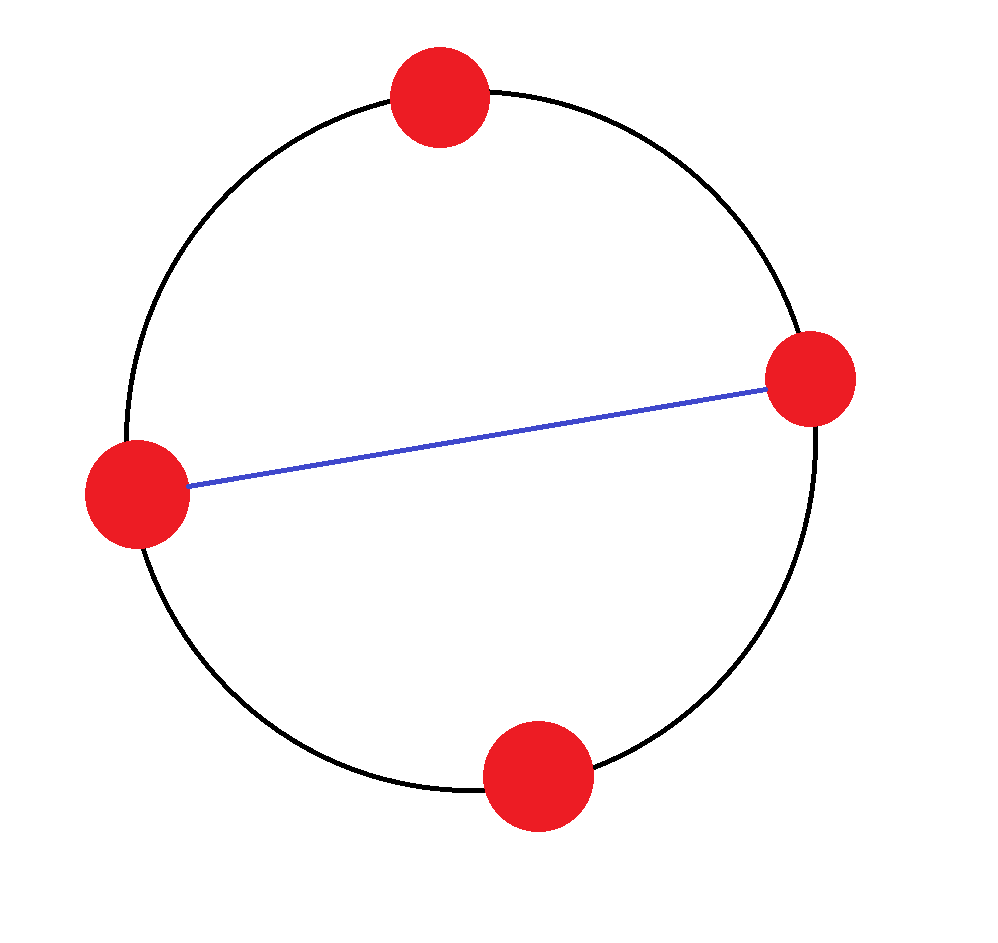
만일 이렇게 잇게 된다면 양 끝에 공이 홀수 개가 남게 되고, 남은 두 공을 잇게 된다면 가운데 있는 선분과 교차하게 되므로 가짓수는 0개이다.
마지막으로 원주에 공이 6개 있을 때는

이와 같이 나오게 되는데, 첫 번째 쌍을 다음과 같이 이었을 때를 생각해보자.

문제에선 두 쌍을 잇는 선분끼리 교차하면 안된다고 했다.
따라서 위 선분을 기점으로 원주에 있는 공들을 2부분으로 나누면, 2개, 2개로 나뉘어지고, 아까 원주에서 공이 2개 있을 때 제작 가능한 쌍의 경우의 수를 1가지라 했으므로 위와 같이 선분을 이었을 땐 (1*1=1)가지의 경우가 나온다.
다음과 같은 경우도 생각해보자.

위와 같이 선분을 그었을 땐 원주에 공이 4개 있을 때 제작 가능한 쌍의 경우의 수 * 1을 해주면 되므로, 이 때 나올 수 있는 경우의 수는 총 2가지이다.
이런 식으로 처음 그은 선분을 기준으로 원을 나눠 dp스럽게 문제를 해결하면 원주에 공이 8개 있을 때는 14가지라는 답이 나오게 된다.
-5번 문제

일단 검은 공을 꺼냈으므로, 꺼낸 공의 위치가 A일 확률은 배제시켜야 한다.
그 후, B일 확률, C일 확률, D일 확률을 따로따로 계산해주면 된다.
꺼낸 검은 공의 위치가 B일 확률은 (1/전체 검은 공)의 개수이고, 이 상태에서 또다시 검은 공을 뽑게 될 확률은 0이므로 (1/6)*0을 답에 더해준다.
그 다음 꺼낸 검은 공의 위치가 C일 확률은 (2/전체 검은 공의 개수)이고, 이 상태에서 또다시 검은 공을 뽑게 될 확률은 1/2이므로 (2/6)*(1/2)를 답에 더해준다.
그 다음 껀낸 검은 공의 위치가 D일 확률은 (3/전체 검은 공의 개수이고), 이 상태에서 또다시 검은 공을 뽑게 될 확률은 1이므로 (3/6)*1을 답에 더해준다.
따라서 답은 (1/6)+(1/2) = (2/3)이 된다.
-6번 문제

이 문제는 높이가 가장 긴 막대기를 기준으로 나올 수 있는 경우의 수를 계산하면 편하다.
그 이유는 왼쪽에서 봤을 때는 가장 긴 막대기 이후에 배치된 막대기는 절대로 볼 수 없고, 오른쪽에서 봤을 대는 가장 긴 막대기 이전에 배치된 막대기를 절대로 볼 수 없기 때문이다.
일단 가장 긴 막대기는 왼쪽에서 봤을 때 3개의 막대기, 오른쪽에서 봤을 때 2개의 막대기가 보여야 한다는 조건 때문에 3번째, 4번째, 5번째 위치에 위치할 수 있다.
3번째 위치에 위치했을 때부터 생각해보자.
3번째 위치에 위치하면, 왼쪽에서 3개의 막대기가 보여야 하기 때문에 왼쪽에서 나올 수 있는 경우의 수는 완전히 정렬된 상태의 1가지 경우밖에 안 나오고, 오른쪽에서 나올 수 있는 경우의 수는 오른쪽에 가장 긴 막대기를 배치하고 나머지는 마음대로 정렬한 2!가지의 경우의 수가 나온다.
따라서 이 경우엔 총 (5C2)*1*2 = 20가지의 경우가 나오게 된다.
다음으로 4번째 위치에 있을 때는 가장 긴 막대기를 기준으로 오른쪽에 있는 막대기들을 세우는 방식은 똑같지만, 왼쪽에 있는 막대기들을 세우는 방식이 더 다양해졌다.
왼쪽에 있는 막대기들을 왼쪽에 있는 막대기들 중에서 가장 긴 막대기를 기준으로 분할해 생각하자.
왼쪽에서 총 3개의 막대기가 보여야 하므로 가장 긴 막대기가 가장 왼쪽에 있을 순 없고, 두 번째, 세 번째 칸에 있을 수 있다.
두 번째 칸에 있을 때는 남은 2개의 막대기를 마음대로 정렬할 수 있어 2!가지의 경우의 수가 나오고, 세 번째 칸에 있을 때는 남은 2개의 막대기 중 더 큰 막대기를 앞에 세워야 왼쪽에서 4개의 막대기가 보이는 불참사를 막을 수 있기 때문에 1가지의 경우만 존재하게 된다.
따라서 이 경우엔 총 (5C2)*(2+1)*1 = 30가지의 경우가 나오게 된다.
마지막으로 5번째 위치에 있을 때는 마찬가지로 가장 긴 막대기를 기준으로 오른쪽에 있는 막대기들을 세우는 방식은 똑같지만, 왼쪽에 있는 막대기들을 세우는 방식이 훨씬 다양해졌다.
이번에도 왼쪽에 있는 막대기들을 왼쪽에 있는 막대기들 중에서 가장 긴 막대기를 기준으로 분할해 생각해보자.
마찬가지로 왼쪽에서 가장 긴 막대기가 가장 왼쪽에 있으면 왼쪽에서 2개의 막대기밖에 보이지 않기 때문에 두 번째, 세 번째, 네 번째 위치에 있을 수 있다.
이 막대기가 두 번째 위치에 있을 때는 첫 번째 위치에 왼쪽에 있는 어떤 막대기가 와도 조건이 성립되므로 3!가지가 나오게 된다.
세 번째 위치에 있을 때는 이 막대기를 기준으로 왼쪽에 있는 막대기들 중 제일 긴 막대기가 앞에 와야 4개가 보이는 불참사를 막을 수 있어 총 (3C1)*1가지가 나오게 된다.
네 번째 위치에 위치에 있을 때도 마찬가지로 이 막대기를 기준으로 왼쪽에 있는 막대기들 중 제일 긴 막대기가 첫 번째 칸에 와야 4개~5개가 보이는 불참사를 막을 수 있어 2!가지가 나오게 된다.
따라서 이 경우엔 총 (5C1)*(6+3+2) = 55가지의 경우가 나오게 된다.
위에서 구한 세 경우의 모든 경우의 수를 더하면 105가지가 나오고, 이게 문제의 답이 된다.
-7번 문제

위의 수들 중 절댓값이 가장 큰 순서대로 나열하면 -7, -6, 6 ... 이 순서대로 나열되게 된다.
-에 -를 곱하면 +가 되므로 -7*-6*6 = 252가 최댓값이 된다.
-8번 문제

일단 2310을 소인수분해 해보았다.
2310=2*3*5*7*11으로 소인수분해가 되었고, 이를 세 개의 집합으로 나누는 문제였다.
그러나, a<b<c였기 때문에 순열이 아닌 조합을 구해야했고, a 집합은 언제나 2를 포함한다고 가정하고 나머지 b, c를 구해 b, c의 중복만 고려해도 문제가 풀리도록 했다.
이렇게만 가정하면 간단해 보이지만, a, b, c 중 하나가 1이 되는 경우의 수도 생각해줘야 한다.
일단 n(a)=1일 때는 (4C1)+(4C2)/2+1가지의 경우가 나왔고,
n(a)=2일 때는 (4C1)*(3C1+1)가지,
n(a)=3일 때는 (4C2)*2가지,
n(a)=4일 때는 (4C1)가지의 경우의 수가 나왔다.
따라서 위 경우의 수를 모두 더하면 40가지의 경우가 나온다.
-9번 문제

이번 문제도 dp였다.
dp[14]를 0으로 정하고 맨 뒤 인덱스(14)부터 시작해 인덱스가 0보다 클 동안 i를 줄여가며 dp에 값을 저장해가면 된다.
dp에 값을 저장할 때는 다음의 점화식으로 저장하면 언제나 최적의 상황을 만들어낼 수 있다.
if(chocolate[i]부터 chocolate[i+2] 중 한 단위 초콜렛만 썩었다면)
dp[i]=max(dp[i], 5+dp[i+3]);
else if(chocolate[i]부터 chocolate[i+2] 중 썩은 단위 초콜렛이 없다면)
dp[i]=max(dp[i], 7+dp[i+3]);
if(chocolate[i]부터 chocolate[i+1] 중 한 단위 초콜렛만 썩었다면)
dp[i]=max(dp[i], 3+dp[i+2]);
else if(chocolate[i]부터 chocolate[i+1] 중 썩은 단위 초콜렛이 없다면)
dp[i]=max(dp[i], 4+dp[i+2]);위 점화식으로 dp[1]을 구하면, 그 값이 정답이 된다.(답 = 25)
-10번 문제

위 문제는 수학 문제를 가장한 순열 사이클 분할 문제였다.
순열에서의 한 사이클을 예시로 들어 설명해보자.
10(a[1]) -> 4(a[10]) -> 2(a[4]) -> 1(a[2]) 이런 사이클이 존재하는데, 문제를 조금 변형해 해석하자면,
int temp=a[1];
a[1]=a[10];
a[10]=a[4];
a[4]=a[2];
a[2]=temp;이런 식으로 변형해 생각할 수 있으므로, 매번 현재 순열에 a를 곱할 때마다 저 사이클을 한 칸씩 돈다고 생각할 수 있다.
따라서 일단 순열에 존재하는 모든 사이클을 구해보았다.
10 -> 4 -> 2 -> 1 -> 10 ...
15 -> 12 -> 7 -> 13 -> 3 ->15 ...
9 -> 5 -> 9 ...
6 -> 6 ...
14 -> 11 -> 8 -> 14 ...
이런 식으로 모든 사이클을 구해보았다.
위 사이클에선 반복 주기를 찾을 수 있는데, 첫 번째 사이클은 4, 두 번째는 5, 세 번째는 2, 네 번째는 1, 다섯 번째는 3이다.
이런 정보와 최소공배수 개념을 이용해 a^m이 되기 위해 a를 몇 번 제곱해야 하는지 알아낼 수 있다.
일단 (a^m)[1]=2이므로, 첫 번째 사이클은 총 2+4k번 반복됐다는 걸 알 수 있다.
따라서 m은 3, 7, 11, 15, 19 ... 중 하나가 될 수 있다.
다음으로 (a^m)[3]=15이므로, 두 번째 사이클은 총 0+5k번 반복됐다는 걸 알 수 있다.
따라서 m은 1, 6, 11, 16, 21, 26 ... 중 하나가 될 수 있다.
다음으로 (a^m)[5]=9이므로, 두 번째 사이클은 총 0+2k번 반복됐다는 걸 알 수 있다.
따라서 m은 1, 3, 5, 7, 9, 11 ... 중 하나가 될 수 있다.
(a^m)[6]은 언제나 6이므로 신경 쓸 필요가 없고,
(a^m)[8]=8이므로, 세 번째 사이클은 총 2+3k번 반복됐다는 걸 알 수 있다.
따라서 m은 3, 6, 9, 12, 15, 18 ... 중 하나가 될 수 있다.
이제 m의 범위를 조금씩 줄여 나가보자.
일단 세 번째 사이클에 의해 m은 홀수 밖에 될 수 없다.
또한, 다섯 번째 사이클에 의해 m은 홀수인 3의 배수 밖에 될 수 없고,
첫 번째 사이클에 의해 m은 3, 15, 27, 39, 51 등...이 될 수 있다.
마지막으로 두 번째 사이클에 의해 m의 일의 자리는 1이나 6밖에 될 수 없으므로 답은 51이 된다.
-11번 문제

이 문제도 dp였다...
왜 이렇게 dp가 많이 나오는지...
어쨌든 풀이를 시작해보자.
dp라서 개념만 확인하면 되니 점화식부터 알아보자.
이 문제도 전 문제들처럼 dp배열의 맨 뒤에서부터 특정 칸에 있을 때 누가 이기는지 계속 확인해나가며 dp배열을 채워나가면 된다.
dp[i]를 채울 때는 다음과 같은 점화식에 따라 채우면 되며, dp[k]는 0으로 채우고 시작한다.
(0의 의미는 이 칸에서 움직이는 사람이 승리한다는 의미이고, 1의 의미는 이 칸에서 움직이는 사람이 패배한다는 의미이다.)
if(dp[i+1]==1||dp[i+2]==1||dp[i+3]==1) //현재 칸에서 움직일 수 있는 칸 중 1이 들어있는 칸이 있다면
dp[i]=0;
else
dp[i]=1;위와 같은 점화식이 나온 이유는 자신이 특정 칸에서 움직여서 도착한 칸이 1이라면 그 칸에서 상대방이 다음 칸으로 움직일 때 어떻게 움직이든 나한테 지게 되어있다는 뜻이기 때문이다.
따라서 현재 칸에서 움직일 수 있는 칸 중 1인 칸이 있다면 0으로 처리해줄 수 있다.
이 일련의 과정을 거친 후, dp[0]이 0이라면 영희가 이긴다 하면 되고, dp[0]이 1이라면 철수가 이긴다고 하면 된다.
-12번 문제


철수가 위에 나온 방식대로 이동하되, 어떤 경로로 이동하든 아이템을 한 개만 수령하게 하고 싶으면 다음과 같은 방식으로 아이템을 배치하면 된다.
| 시작 | ITEM | ||||||
| ITEM | |||||||
| ITEM | |||||||
| ITEM | |||||||
| 끝 |
그러나, 위 문제에선 X표시와 함께 철수가 갈 수 없는 영역이라고 표시해두었다.
따라서 우린 경우의 수를 좀 더 세세히 따져줄 필요가 있다.
일단 X표시가 있든 없든 다음과 같은 세가지 방법은 동일하다.
| 시작 | ITEM | ITEM | ITEM | ||||
| ITEM | ITEM | ITEM | X | X | |||
| ITEM | ITEM | X | X | ||||
| ITEM | |||||||
| X | X | ||||||
| X | X | ||||||
| 끝 |
그 후, 범위의 왼쪽 끝은 다음 6개 경우 중 하나,
| 시작 | |||||||
| X | X | ||||||
| X | X | ||||||
| O | X | X | |||||
| O | X | X | |||||
| O | O | O | O | 끝 |
범위의 오른쪽 끝은 다음 6개 경우 중 하나가 되면
| 시작 | O | O | O | O | |||
| X | X | O | O | ||||
| X | X | O | |||||
| X | X | ||||||
| X | X | ||||||
| 끝 |
아이템을 가운데에 배치할 경우의 수는 다음과 같이 6가지가 나온다.
| 시작 | |||||||
| O | X | X | |||||
| O | O | O | X | X | |||
| O | O | O | O | O | O | ||
| X | X | O | O | ||||
| X | X | O | |||||
| 끝 |
따라서 현재까지 센 경우의 수는 총 3+6*6*6 = 219가지이다.
또한, 다음과 같은 3가지 경우도 존재한다.
| 시작 | |||||||
| X | X | ||||||
| X | X | ||||||
| O | |||||||
| X | X | O | O | ||||
| X | X | O | O | O | |||
| O | O | O | 끝 |
따라서 모든 경우의 수는 222가지가 되는 것처럼 보인다.
그러나, 다음 두 위치의 경우 철수가 도달할 수 없거나 도달해도 더이상 움직일 수 없기 때문에 아무렇게나 아이템을 배치해도 상관이 없다.
| 시작 | |||||||
| X | X | ||||||
| X | X | ||||||
| O | X | X | |||||
| X | X | O | |||||
| 끝 |
따라서 위에서 구한 경우의 수에 2*2를 곱해 총 888가지의 경우의 수가 나오게 된다.
'mathematics' 카테고리의 다른 글
| 분할 정복을 이용한 행렬 거듭 제곱 (2) | 2023.02.27 |
|---|---|
| 수학 - 자이스토리 1등급 고난도 스토리 197번 (0) | 2022.06.06 |
| 수학 - 자이스토리 1등급 고난도 스토리 191번 (0) | 2022.06.06 |